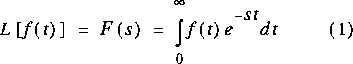
CIRCUITS
Définition:
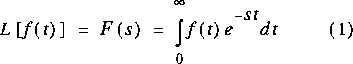
1. Que f(t) soit continue par section pour tout intervalle t >= 0.En fait ces conditions imposent la convergence de l'intégrale (1).2. Que
, i.e. il faut que M et alpha existent.
La transformée inverse se dénote:
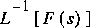
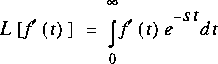
Generated with CERN WebMaker