[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 19: Transformation de Laplace. (p. 623)
19.3 Convolution (p.635).
À cause de la linéarité, on retrouve souvent le produit de 2 fonctions.
Ex: P=VI,...
Si on a:
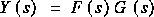
il faut absolument trouver l'inverse, c'est-à-dire:
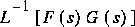
Cette transformation inverse s'appelle la convolution.

Si on change l'ordre d'intégration, et comme  ,
on a:
,
on a:

Ce qui, d'après la définition de la transformée est:
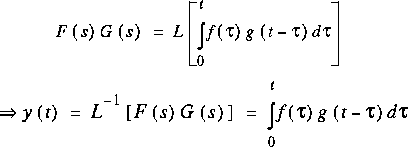
Ce résultat est le théorème de la convolution:
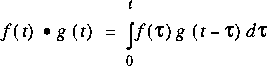
L'ordre de f et g n'a pas d'importance, comme on peut le démontrer.
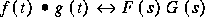
Une convolution dans le domaine temporel équivaut à une multiplication en temps.
Même si on peut employer le théorème de convolution pour calculer des transformées, ce n'est pas une bonne approche car les calculs deviennent vite trop complexes.
Analyse graphique de la convolution.
Supposons 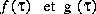 comme ceci:
comme ceci:
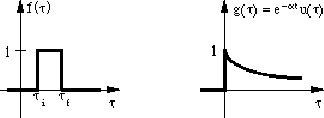
Si on décale 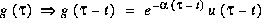 .
.
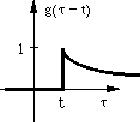
Changeons maintenant le signe de l'argument et l'argument de l'intégrale de convolution.
Pour 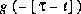 , les valeurs négatives le long de l'axe
, les valeurs négatives le long de l'axe  donnent les mêmes valeurs que les valeurs positives pour la fonction non renversée. La fonction se trouve à être comme repliée sur elle-même en "miroir".
donnent les mêmes valeurs que les valeurs positives pour la fonction non renversée. La fonction se trouve à être comme repliée sur elle-même en "miroir".
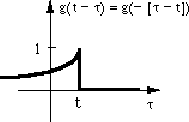
 sera nul seulement lorsque les 2 fonctions seront superposées.
sera nul seulement lorsque les 2 fonctions seront superposées.

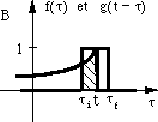
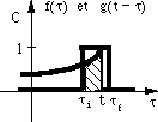
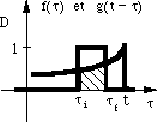
Les graphes A à D montrent les cas possibles pour différentes valeurs de t et l'intégrale correspond à la surface sous la courbe. Si on calcule cette surface pour toutes les valeurs de t, on trouve:

Ce qui correspond à l'intégrale de convolution, donc, à la convolution.
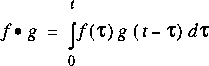
Note: Si on avait décalé et renversé  plutôt que
plutôt que 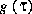 , on aurait obtenu le même graphique. La convolution est un important outil de simulation.
, on aurait obtenu le même graphique. La convolution est un important outil de simulation.
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker
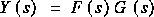
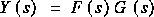
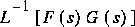

 ,
on a:
,
on a:
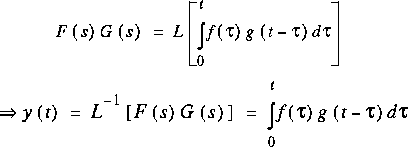
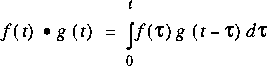
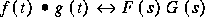
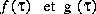 comme ceci:
comme ceci: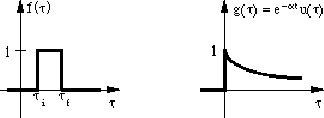
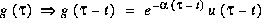 .
.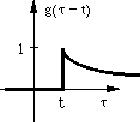
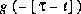 , les valeurs négatives le long de l'axe
, les valeurs négatives le long de l'axe  donnent les mêmes valeurs que les valeurs positives pour la fonction non renversée. La fonction se trouve à être comme repliée sur elle-même en "miroir".
donnent les mêmes valeurs que les valeurs positives pour la fonction non renversée. La fonction se trouve à être comme repliée sur elle-même en "miroir".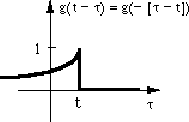
 sera nul seulement lorsque les 2 fonctions seront superposées.
sera nul seulement lorsque les 2 fonctions seront superposées.
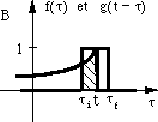
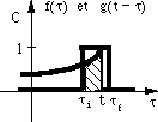
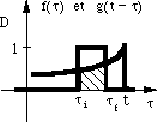

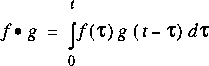
 plutôt que
plutôt que 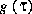 , on aurait obtenu le même graphique. La convolution est un important outil de simulation.
, on aurait obtenu le même graphique. La convolution est un important outil de simulation.