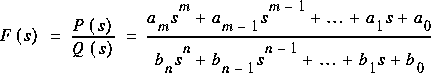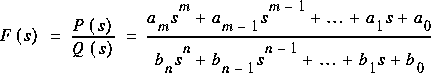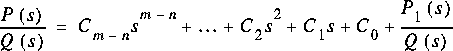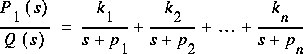[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 19: Transformation de Laplace. (p. 623)
19.5 Transformée inverse (p.646).
Comme on l'a dit, le but ultime de l'étude de la transformée de Laplace, c'est la résolution de circuits. La solution algébrique de l'équation d'un circuit dans le domaine de la transformée donnera une fonction rationnelle de la forme suivante:
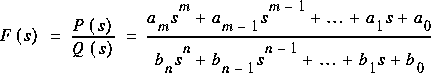
- Les racines de P(s) sont appelées les zéros de F(s) car, pour ces valeurs F(s) = 0.
- Les racines de Q(s) sont appelées pôles de F(s) car, pour ces valeurs F(s) devient infini.
Normalement, n > m. Si ce n'est pas le cas, on divise P(s) par Q(s):
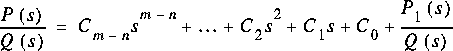
* Le degré de Q(s)< est plus grand que celui de P1(s).
Examinons les formes possibles des racines de Q(s), donc les pôles. (Cette étude est très importante.)
1. Les pôles sont simples (i.e. tous différents, de multiplicité = 1 et réels), on peut décomposer.
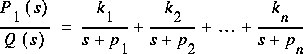
La décomposition est simple.

2. Q(s) a des pôles complexes qui apparaissent sous la forme de paire complexes conjuguées.
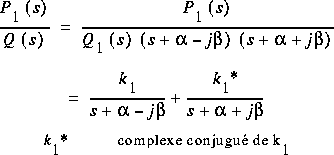
3. Si Q(s) a des pôles de multiplicité n, la décomposition sera de la forme

L'importance de ces techniques de décomposition vient de la facilité avec laquelle on peut alors passer à la transformée inverse: il suffit de consulter une table.
Note: Si on a:
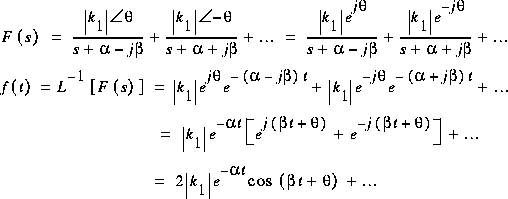
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker