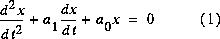
Chapitre 9: Circuits de 2ième ordre
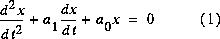
Essayons  (2), et remplaçons (2) dans (1)
(2), et remplaçons (2) dans (1)

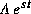 ne peut être nul, on ne pourrait satisfaire les conditions initiales.
ne peut être nul, on ne pourrait satisfaire les conditions initiales.
->Il faut 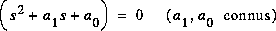 . C'est l'équation caractéristique obtenue en remplaçant les dérivées par les puissances de s.
. C'est l'équation caractéristique obtenue en remplaçant les dérivées par les puissances de s.
On a les 2 solutions:

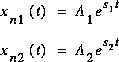
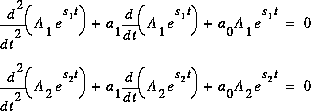
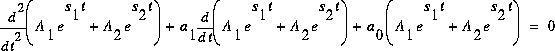
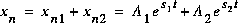
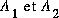 sont obtenus des conditions initiales.
sont obtenus des conditions initiales.
Generated with CERN WebMaker