[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 9: Circuits de 2ième ordre
9.4 Les 3 types de réponses naturelles (p. 267)
Cela dépend des racines de l'équation caractéristique, il y a 3 cas:
- racines réelles distinctes.
- racines complexes.
- racines identiques.
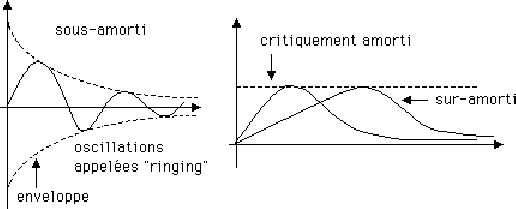
Racines réelles distinctes: Cas sur-amorti (overdamped). La réponse décroît et s'atténue.
Racines complexes: Cas sous-amorti (underdamped).
On a:

Note: Dans ce cas 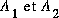 seront aussi des nombres complexes et il est plus commode de passer en coordonnées polaires avec la règle d'Euler:
seront aussi des nombres complexes et il est plus commode de passer en coordonnées polaires avec la règle d'Euler:
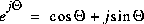
donc:

Pour un circuit, 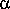 < 0, on aura donc une réponse oscillatoire et amortie.
< 0, on aura donc une réponse oscillatoire et amortie.
Racines réelles identiques: Amortissement critique (critically damped case). On a: 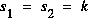 , c'est le cas limite des 2 précédents. L'équation caractéristique a la forme:
, c'est le cas limite des 2 précédents. L'équation caractéristique a la forme:
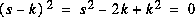
Cette fois on a:

Cette forme n'est généralement pas la bonne car elle ne peut pas satisfaire les 2 conditions initiales avec une seule constante 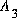 .
.
Essayons une forme plus générale: 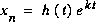 , avec:
, avec:
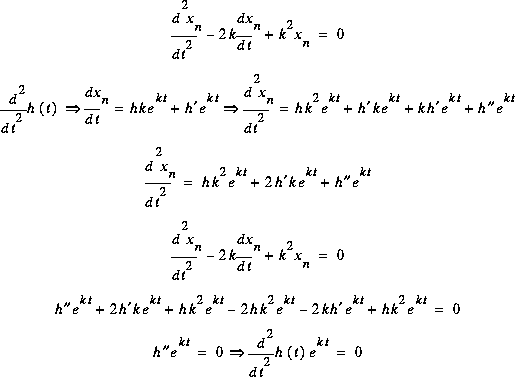
Il faut que h(t) soit telle que sa 2e dérivée soit nulle pour tout t. C'est vrai si h(t) est un polynôme de 1er ordre.

Donc la solution générale pour le cas de 2 racines réelles distinctes 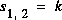 est:
est:
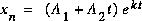
Graphiquement, on a donc les 3 cas:
Note: 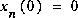
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker


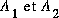 seront aussi des nombres complexes et il est plus commode de passer en coordonnées polaires avec la règle d'Euler:
seront aussi des nombres complexes et il est plus commode de passer en coordonnées polaires avec la règle d'Euler: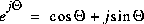

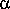 < 0, on aura donc une réponse oscillatoire et amortie.
< 0, on aura donc une réponse oscillatoire et amortie.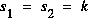 , c'est le cas limite des 2 précédents. L'équation caractéristique a la forme:
, c'est le cas limite des 2 précédents. L'équation caractéristique a la forme: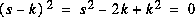

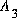 .
.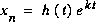 , avec:
, avec: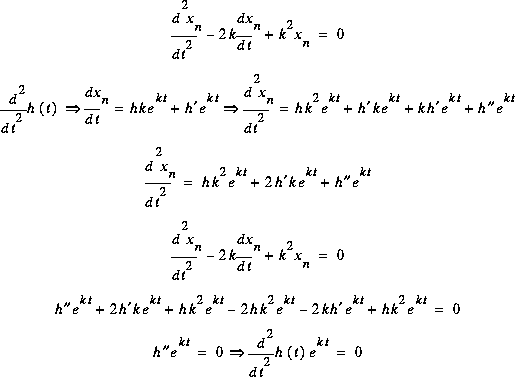

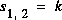 est:
est: