[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 8: Réseaux RC et RL simples (p.207)
8.3 Circuit RL sans source (p.216)
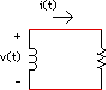
Convention:
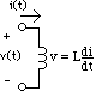
Énergie emmagasinée à t = 0 (inductance chargée avec 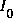 ):
):
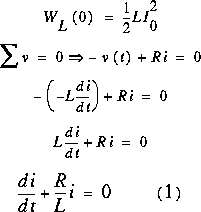
C'est le même type d'équation que pour un condensateur. Cette fois, on emploie une méthode où l'on assume la réponse pour la trouver, comme en Calcul II.
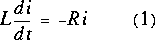
Posons (2), une fonction qui garde sa forme même en étant différentiée:
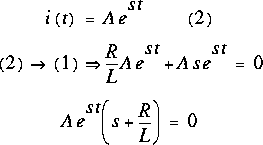
On a 2 choix:
1. 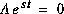 , ce n'est pas un bon choix car alors i(t) = 0 pour tout t, ce qui est en contradiction avec
, ce n'est pas un bon choix car alors i(t) = 0 pour tout t, ce qui est en contradiction avec  .
.
2. s = -R/L, choix qui est retenu.
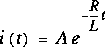
et comme  .
.

Unités:
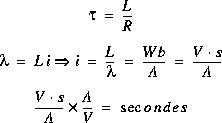
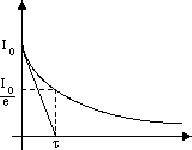
On a un graphe de la même forme:
Puissance instantanée fournie à la résistance:
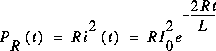
Énergie totale:
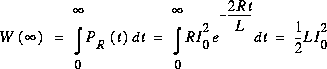
Comme prévu, toute l'énergie emmagasinée dans l'inductance est dissipée par la résistance.
Si on avait voulu trouver la tension à l'inductance:
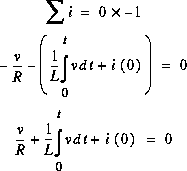
Dérivons par rapport au temps:
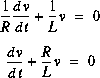
Cette équation peut être résolue comme précédemment.
Si on remplace v par Ri, on retrouve:
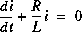
Note: Même si pour l'inductance 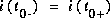 , pour les résistances, il y a un saut abrupt de la valeur du courant.
, pour les résistances, il y a un saut abrupt de la valeur du courant.
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker
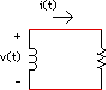
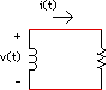
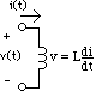
 ):
):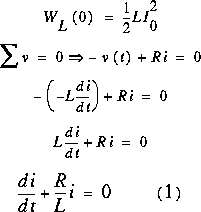
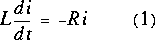
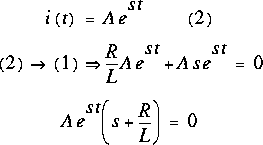
, ce n'est pas un bon choix car alors i(t) = 0 pour tout t, ce qui est en contradiction avec
.
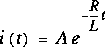
 .
.
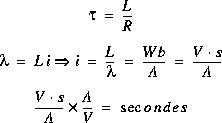

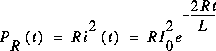
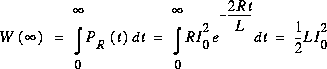
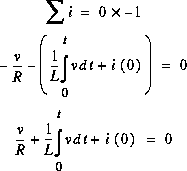
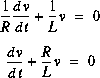
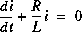
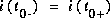 , pour les résistances, il y a un saut abrupt de la valeur du courant.
, pour les résistances, il y a un saut abrupt de la valeur du courant.