[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 6: Équations indépendantes (p. 151)
6.2 Équations indépendantes de courant
Nous allons voir une méthode systématique de résolution pour un circuit ayant N noeuds et B branches. Nombre de liens = branches du graphe - branches de l'arbre. #liens = B - (N - 1).
liens = B - N + 1
Raisonnement: Prenons l'arbre d'un circuit si on force à zéro tous les courants de lien (remplaçons les liens par des circuits ouverts). Puisque l'arbre ne contient aucune boucle fermée, tous les courants de boucle sont nuls. Donc, les courants de branche sont dépendants des courants de lien. De plus, si un courant de lien n'est pas forcé à zéro, un courant circulera (puisqu'avec un lien, une boucle est formée dans l'arbre). On en conclut que les courants de lien sont indépendants. On aura:
- (B-N+1) courants de liens - (nombre de sources courant dans le circuit)
- (B-N+1) équations indépendantes - (nombre de sources courant dans le circuit)
Méthode:
1. On part de l'arbre, on rajoute un lien. On obtient une boucle, on peut appliquer la loi des tensions.
2. On recommence (B - N + 1) fois, pour obtenir (B - N + 1) équations indépendantes.
Note: Les sources de courant doivent être remplacées par des liens car les liens font référence aux courants indépendants du circuit.
On place généralement les sources de tension dans les boucles.
A retenir de ce chapitre (2 relations très utiles pour déterminer la méthode la plus efficace pour la résolution d'un circuit):
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker
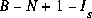 équations dans le circuit, où
équations dans le circuit, où 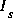 est le nombre de sources de courant indépendantes ou dépendantes présentes dans le circuit.
est le nombre de sources de courant indépendantes ou dépendantes présentes dans le circuit.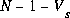 équations dans le circuit,
où
équations dans le circuit,
où 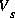 est le nombre de sources de tension indépendantes ou dépendantes présentes dans le circuit.
est le nombre de sources de tension indépendantes ou dépendantes présentes dans le circuit.