Chapitre 6: Équations indépendantes (p. 151)

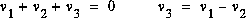
 : tensions de branches, et
: tensions de branches, et 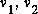 : tension de lien. Elles ne sont donc pas indépendantes.
: tension de lien. Elles ne sont donc pas indépendantes.
Les tensions des N - 1 branches sont indépendantes puisque si on force toutes les autres à zéro, celles-ci demeurent. Exemple: Si  demeure:
demeure:
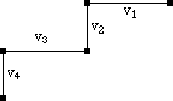
1. Faire le graphe du circuit.Note: La résolution devient simple mais il faut:2. Dessiner un graphe (branches et liens).
3. Indiquer les inconnues sur l'arbre (branches et liens). Il y en a (N-1) - (nombre de sources de tension).
4. Isoler une branche de l'arbre, l'arbre est alors sectionné en deux parties, on calcule par la loi des courants, le courant qui passe d'une partie à l'autre, ce qui nous donne une équation.
5. On reprend "4" pour toutes les branches à déterminer.
6. Le circuit est complètement caractérisé.
1. Choisir l'arbre judicieusement (inclure toutes les sources).2. Le couper judicieusement de façon à pouvoir calculer facilement les courants, en évitant les sources de tension.
Generated with CERN WebMaker