rad/s correspondent à de grandes amplitudes, celles près de 
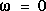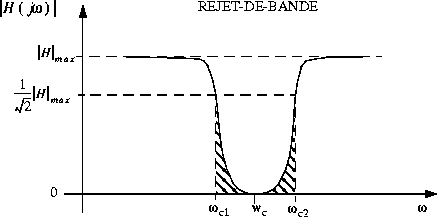
ou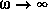 
à de petites amplitudes. C'est l'illustration d'un filtre "PASSE-BANDE" qui laisse passer une "bande de fréquence" centrée autour de 
.
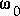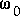est appelée "fréquence centrale".
Chapitre 20: Réponse en fréquence
rad/s correspondent à de grandes amplitudes, celles près de
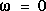ou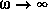
à de petites amplitudes. C'est l'illustration d'un filtre "PASSE-BANDE" qui laisse passer une "bande de fréquence" centrée autour de
.
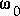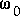est appelée "fréquence centrale".
où,
sont les fréquences de coupure ("cutoff").
est appelée largeur de bande ou "bandwidth".
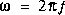, f étant la fréquence en Hz.
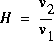, (i.e. la réponse en fréquence).
, 
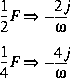
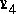, et employons le sens conventionnel des courants.
.
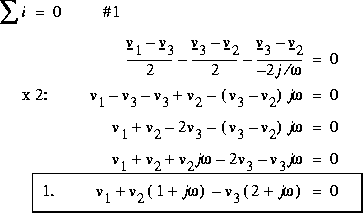
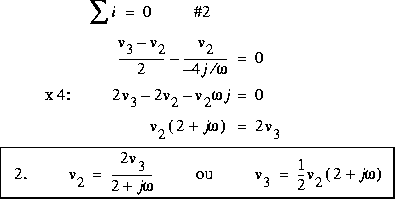
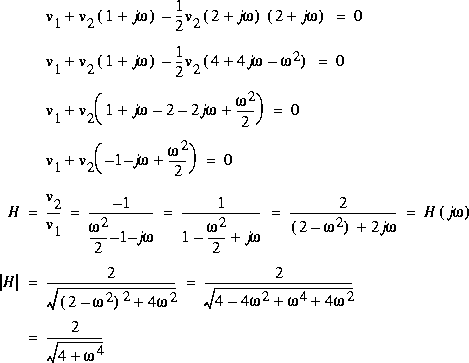
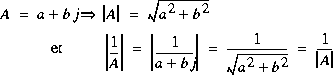
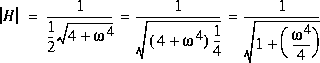
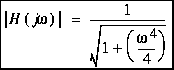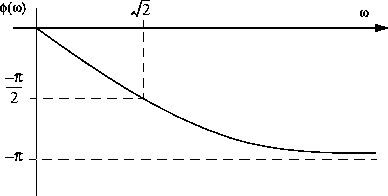
On remarque que l'amplitude décroît continuellement lorsque la fréquence
Rappel:
Les deux filtres vus précédemment sont du second ordre. Un ordre plus élevé permet une meilleure réponse en fréquence, mais ils sont aussi plus coûteux à fabriquer (car ils exigent plus de composants).
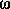augmente. En fait, 
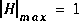à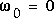 
. La réponse est: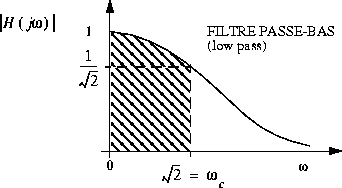
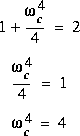
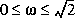
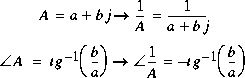
En général, l'ORDRE D'UN FILTRE est donné par le degré du polynôme au dénominateur de la fonction H.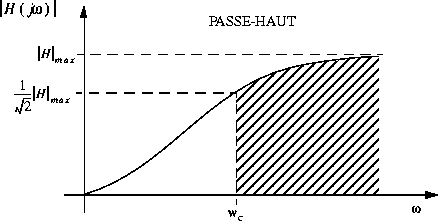
CIRCUITS - 21 JUN 96
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker