Chapitre 20: Réponse en fréquence
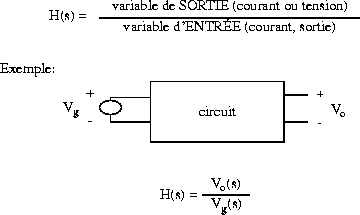
Déf.: La fonction de transfert d'un réseau, c'est le rapport entre le phaseur d'excitation d'entrée sur le phaseur de réponse (sortie), on l'exprime généralement par la lettre H(s):

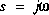 où
où  .
.
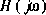 est généralement une fonction complexe avec partie réelle et imaginaire:
est généralement une fonction complexe avec partie réelle et imaginaire:
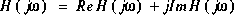 forme cartésienne
forme cartésienne
 forme polaire
forme polaire
où:
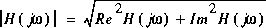
et: 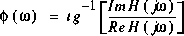
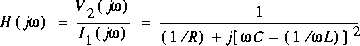
avec: 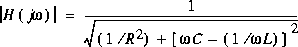
et: 
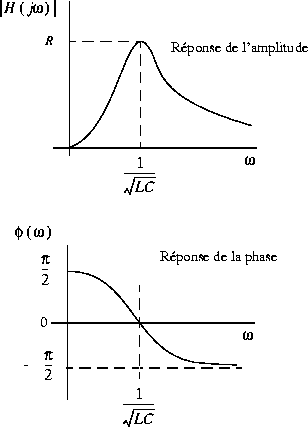
Puisque R, L et C sont des constantes, l'amplitude maximale s'observe à la fréquence 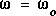 , pour laquelle le dénominateur de l'expression de
, pour laquelle le dénominateur de l'expression de 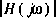 est minimum. Cela survient de façon évidente lorsque:
est minimum. Cela survient de façon évidente lorsque:
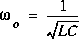
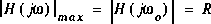 .
. si
si  ou
ou  . On peut alors tracer la réponse de l'amplitude. De la même façon, on peut tracer la réponse de la phase puisque
. On peut alors tracer la réponse de l'amplitude. De la même façon, on peut tracer la réponse de la phase puisque 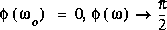 lorsque
lorsque 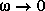 et
et 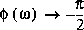 si
si  .
.
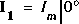 (i.e. dans le domaine temporel:
(i.e. dans le domaine temporel:  ), alors le phaseur de sortie sera
), alors le phaseur de sortie sera 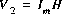 . Comme on peut le constater, on obtient autant d'information à partir de la fonction de transfert du réseau qu'à partir de la réponse de sortie (à condition de connaître l'excitation d'entrée). Pour cette raison, et aussi parce que la fonction de transfert du réseau ne dépend que des éléments du réseau et de leurs connexions respectives (et non de la façon dont il est excité), nous ne considérerons que la réponse en fréquence de la fonction de transfert du réseau.
. Comme on peut le constater, on obtient autant d'information à partir de la fonction de transfert du réseau qu'à partir de la réponse de sortie (à condition de connaître l'excitation d'entrée). Pour cette raison, et aussi parce que la fonction de transfert du réseau ne dépend que des éléments du réseau et de leurs connexions respectives (et non de la façon dont il est excité), nous ne considérerons que la réponse en fréquence de la fonction de transfert du réseau.
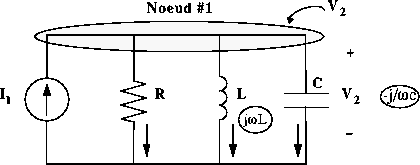
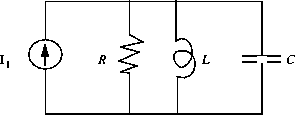
 au noeud #1, alors :
au noeud #1, alors :

Generated with CERN WebMaker