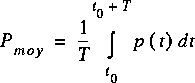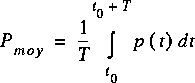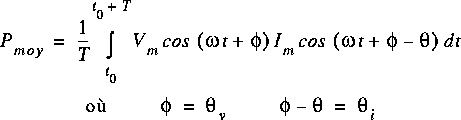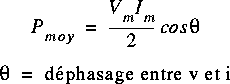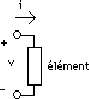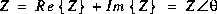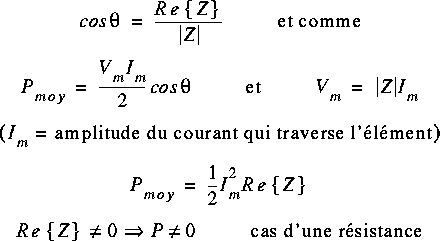[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 12: Puissance en régime sinusoïdal permanent. (chap. 11, p. 429)
12.1 Puissance moyenne (p. 377)
Puissance instantanée:
p(t) = v(t) i(t).
avec v(t) et i(t) périodiques de période T.
p(t+T) = v(t+T) i(t+T) = v(t) i(t) = p(t).
Donc, la puissance est aussi une fonction périodique.
La puissance moyenne est définie comme:
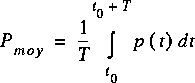
Avec T = période de v où i et t0 = instant arbitraire. Pmoy est la puissance moyenne et p(t) est la puissance instantanée.
Dans le cas de signaux sinusoïdaux:
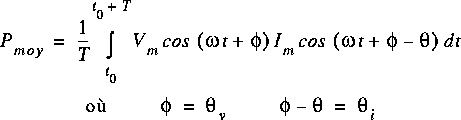
Note: Voir aussi le recueil de Formules du Chapitre 12, p. 115.
Ce qui donne après simplification:
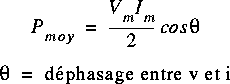
C'est la puissance moyenne absorbée par un élément à 2 bornes.
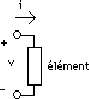
Pour une résistance, il n'y a aucun déphasage entre v et i:

Pour une inductance, theta = 90 (déphasage entre v et i). Pour un condensateur, theta = -90 (déphasage entre v et i). Or, cos(90) = cos(-90) = 0, donc:
Pcondensateur = Pinductance = 0
Donc, un circuit composé uniquement de condensateurs et d'inductances idéaux (sans résistance parasite) ne dissipe aucune énergie. Physiquement, une inductance ou un condensateur absorbe de l'énergie pendant un intervalle de temps, puis, la restitue dans l'intervalle suivant, le bilan étant nul.
En coordonnées cartésiennes, l'impédance 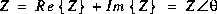

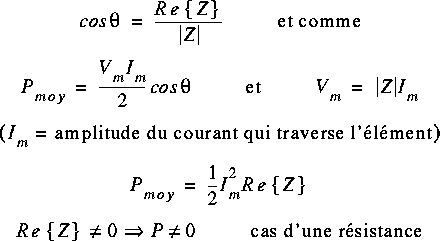
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker