[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Chapitre 10: Excitation sinusoïdale & phaseurs (p. 307)
10.3 Méthode de résolution employant les nombres complexes (p. 314)
Rappel sur les nombres complexes.
Sous forme cartésienne, A = a+jb, avec
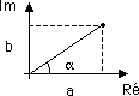
- a: partie réelle (a = Ré[A])
- b: partie imaginaire (b = Im[A]), et
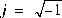
Sous forme polaire:
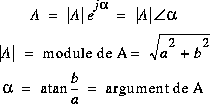
Dans le plan complexe:
Quelques résultats intéressants:

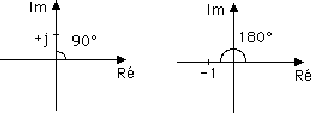
Avec la formule d'Euler, on a que:
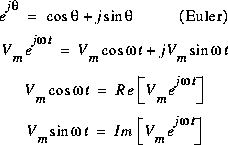
On a constaté précédemment que les exponentielles sont plus faciles à traiter que les sinusoïdes.
Retournons à l'exemple précédent:
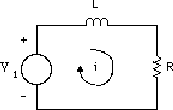
Appliquons l'excitation complexe 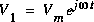 au lieu de l'excitation réelle. C'est un concept abstrait qu'on ne peut pas reproduire en laboratoire, mais, cela simplifie nos calculs. Reprenons l'équation précédente:
au lieu de l'excitation réelle. C'est un concept abstrait qu'on ne peut pas reproduire en laboratoire, mais, cela simplifie nos calculs. Reprenons l'équation précédente:
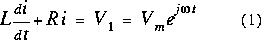
Pour résoudre, posons:
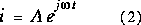
et remplaçons (2) dans (1).

Donc 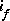 est de la forme:
est de la forme:
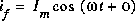
C'est ce que nous avions obtenu pour 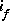 (avec
(avec  ) précédemment. C'est un résultat très intéressant!!
) précédemment. C'est un résultat très intéressant!!
Si 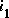 : réponse complexe à l'excitation complexe forcée
: réponse complexe à l'excitation complexe forcée 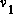 , alors
, alors 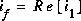 sera la réponse à
sera la réponse à 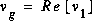 . Ceci est vrai car l'équation différentielle ne contient que des coefficients réels, ce qui sera toujours le cas dans nos circuits.
. Ceci est vrai car l'équation différentielle ne contient que des coefficients réels, ce qui sera toujours le cas dans nos circuits.
CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]
Generated with CERN WebMaker
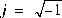
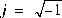
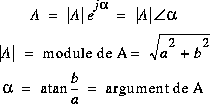


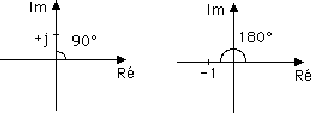
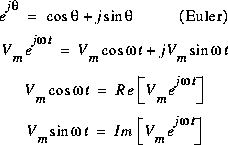

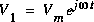 au lieu de l'excitation réelle. C'est un concept abstrait qu'on ne peut pas reproduire en laboratoire, mais, cela simplifie nos calculs. Reprenons l'équation précédente:
au lieu de l'excitation réelle. C'est un concept abstrait qu'on ne peut pas reproduire en laboratoire, mais, cela simplifie nos calculs. Reprenons l'équation précédente: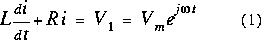
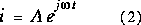

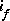 est de la forme:
est de la forme: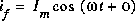
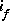 (avec
(avec  ) précédemment. C'est un résultat très intéressant!!
) précédemment. C'est un résultat très intéressant!!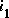 : réponse complexe à l'excitation complexe forcée
: réponse complexe à l'excitation complexe forcée 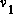 , alors
, alors 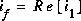 sera la réponse à
sera la réponse à 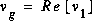 . Ceci est vrai car l'équation différentielle ne contient que des coefficients réels, ce qui sera toujours le cas dans nos circuits.
. Ceci est vrai car l'équation différentielle ne contient que des coefficients réels, ce qui sera toujours le cas dans nos circuits.