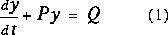
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]

Chapitre 8: Réseaux RC et RL simples (p.207)

8.5 Cas général (p.225)

Ce qu'on a vu jusqu'à présent, ce sont des cas particuliers de:



y = variable inconnue, P, Q = constantes.

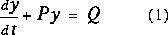
Résolvons cette équation par la méthode des facteurs intégrants, i.e., on multiplie l'équation par un facteur de sorte que le terme de gauche soit un dérivatif parfait.

Dérivons 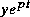selon t:


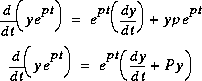
Le facteur 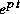permet de simplifier (1). Multiplions donc (1) par .



Intégrons des 2 côtés:



Où A est une constante d'intégration.



Si Q est une constante,



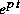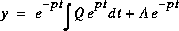
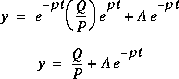
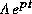Q/P: réponse forcée, : réponse naturelle, et 1/P = = constante de temps de la réponse naturelle.

CIRCUITS - 16 JUL 95
[Page suiv.] [Page préc.] [Niveau préc.] [Notes circuits] [T. matières] [Index]

Generated with CERN WebMaker