Partie A-> Remplacée par son équivalent: une résistance et une source,reste le même.
Chapitre 5 Théorèmes des réseaux (p. 116)
1. Division de tension (directe) et de courant (inverse).
2. Méthode des mailles.
3. Méthode des noeuds.
4. Résistance équivalente.
5. Méthode inverse avec v0 = 1V (homogénéité).
6. Superposition.
Nous allons maintenant en rajouter 2 autres très utiles pour simplifier un circuit.
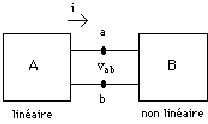
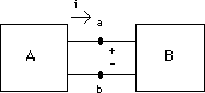
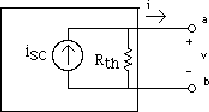
Idée de base: Remplacer tout un circuit, vu d'une paire de bornes, par un circuit équivalent constitué d'une seule résistance et d'une source.
1. On considère que le circuit à simplifier peut être constitué:

Partie A-> Remplacée par son équivalent: une résistance et une source,reste le même.
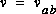 et vu de a, tout reste identique, le courant i reste pareil.
et vu de a, tout reste identique, le courant i reste pareil.
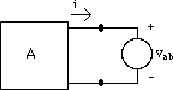

 : courant avec circuit A "mort".
: courant avec circuit A "mort".
 : courant avec source v "morte" (i.e. courant court-circuit).
: courant avec source v "morte" (i.e. courant court-circuit).
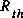 : Résistance thévenin => Toutes les sources à zéro.
: Résistance thévenin => Toutes les sources à zéro.


 , la valeur de la résistance équivalente (circuit purement résistif).
, la valeur de la résistance équivalente (circuit purement résistif).

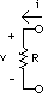




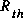 : Résistance thévenin et
: Résistance thévenin et 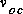 : tension en circuit ouvert.
: tension en circuit ouvert.Vérifions que le circuit correspond bien (boucle):


Generated with CERN WebMaker