Les logarithmes

redbox.gif (41 octets)

Belle invention due à John Napier, (Neper dans d'autres langues) qui publia le premier je crois une table de logarithmes. Quels avantages avons-nous à utiliser les fameux log ? C'est ce que nous allons découvrir. Dernière remarque avant de commencer, il n'est peut-être pas indispensable d'avoir une  maîtrise parfaite des logarithmes pour la licence, ceci dit les notions abordées sont simples et vous seront toujours utiles. Pourquoi s'en priver ?
Avertissement :
Nous ne parlerons ici que du logarithme décimal (en base 10)

 

Et si nous faisions une expérience ?


Pas compliquée et amusante, c'est parti. Vous pouvez la faire temps réel en utilisant la calculatrice Windows (Démarrer - Programmes - Accesoires - Calculatrice).

Nous allons réaliser les opérations suivantes :

Au clavier Afficheur Remarque
1 - Taper 425 425  
2 - Cliquer que la touche Log 2,62838.......... Log en base 10 de 425
3 - Cliquer sur   +  2,62838.......... pour effectuer la somme
4 - Taper 43 43  
5 - Cliquer que la touche Log 1,6334...... Log en base 10 de 43
6 - Cliquer sur   =  4,261857...... la somme des log
7 - Cocher la case  INV    
2 - Cliquer que la touche Log 18275 Le résultat
     

 

Pas parlante mon expérience ? Essayer de taper directement 425 x 43, vous allez trouver 18275. Là vous me prenez pour un fou, car pourquoi faire toutes ces opérations alors qu'une simple multiplication nous apporte une réponse immédiate ?

Quelques éléments de réponse :


Cette expérience ne servait qu'à faire toucher du doigt (au propre comme au figuré) une extraordinaire propriété du log, à savoir qu'une multiplication devient une addition quand on utilise celui-ci. L'affaire ne s'arrête pas là puisqu'une division se transforme en soustraction avec le log.

Voici la courbe de représentative de la fonction Log pour des valeurs partant de 0 à 40 sur l'axe des x. En ordonnée vous trouvez naturellement la valeur Log de 10. Vous constatez que de fortes variations de x se traduisent par de faibles variations de Y. Nous avons une réponse logarithmique. Votre oreille fonctionne comme cela, une forte augmentation de pression ne se traduit pas par une augmentation équivalente de votre perception du son. Cette propriété est très commode en radioélectricité.

Quel avantage à utiliser les logarithmes pour le radio amateur ?



Avant de voir comment les manipuler, voyons un peu ce que cela donne avec un exemple classique. On va y parler de dB (décibel), dans l'immédiat retenez seulement que c'est une application des log. Précisément, il s'agit du logarithme en base 10 d'un rapport qui peut être de puissance ou tension ou encore courant, c'est un moyen extrêmement pratique d'exprimer un rapport de manière logarithmique que nous utiliserons par exemple pour les amplificateurs, les atténuateurs etc.


Nous trouvons une chaîne constituée d'amplificateurs et d'atténuateurs. Pour calculer le gain global (qui peut être une atténuation) et ainsi déterminer la puissance que l'on aura en sortie connaissant la puissance que l'on va y appliquer, sans l'utilisation des log, il faut faire quand même quelques calculs qui, s'ils sont simples, n'en sont pas moins fastidieux. Essayons pour voir :

Voici la chaîne :

Nous devons faire le produit des amplifications, des atténuations et établir le rapport Amplification/atténuation.  Il vient :

Amplification : 10x4x2 =  80
Atténuation : 2 x100 = 200

Rapport :    80/200 = 0,4 
Donc pour synthétiser, si on injecte 1W à l'entrée de cet ensemble, on mesurera 400 mW en sortie...
 



Avec les logarithmes rien de tel, connaissant le gain de chaque sous-ensemble, il nous suffit de faire des additions toutes bêtes. Ex : 10 - 3 + 6  + 3 -20 =  - 4dB. Cette chaîne atténue de 4 dB. C'est quand même bcp plus simple.

A que cela ressemble t-il, une échelle logarithmique ? 
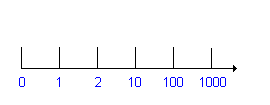  A cela...
Manipulons les logarithmes :
log (a x b) = log a  +  log b
log a / b   =  log a - log b
Moins indispensable pour le moment :
log an = n log a
Quelques exemples avec la calculatrice :


Nous ne calculons qu'en base 10, c'est à dire que sur votre calculette vous n'utilisez que la touche notée LOG et non pas ln. Pour plus d'informations sur les log, allez au chapitre "Décibel"
Quel est le log de 1 ? Log 1 = 0
Quel est le log de 10 Log 10 = 1
Quel est le log de 100 Log 100 = 2
Quel est le log de 1000 Log 1000 = 3
Quel est le log de 10000 Log 10000 = 4
Au passage : tiens, c'est marrant quand même, on dirait que le Log correspond en base 10, à l'exposant qu'il faut appliquer à 10 pour retrouver la valeur du logarithme demandé... Eh bien ceci est vrai dans toutes les bases.


Nous connaissons la valeur du log et nous recherchons la valeur initiale de x:

Log (x) = 2,7201
Pour déterminer x, c'est simple, il suffit de porter 10 (car nous sommes en base10) à la puissance 2,7201.

x  =  102,7201 = 525 (valeur arrondie)
 
 
Quel est le log de 500 ? Log 500 = 2,6989
Quel est le log de 3243 Log 3243 = 3,5109
Quel est le Log de 0,001 Log 0,001 = -3
Quel est le Log de 0,001589 Log 0,001589 = -2,7988
Au passage : vous ne remarquez rien ? Il est facile de déterminer la partie entière d'un log en base 10. 

Juste un mot sur l'exponentielle :


On ne pourrait pas conclure ce rapide survol des logarithmes sans évoquer la fonction réciproque qui est la fonction exponentielle. Ici vous notez qu'une faible variation des X provoque une très grande variations des Y.

Il existe une relation donnée ici pour mémoire seulement qui lie l'exponentielle au logarithme :

log x = y       ey = x

ici log est le log naturel de base e
e est la base (2,72)

 

Nous sommes déjà allés trop loin dans ce chapitre, ne vous cassez pas trop la tête. Ce qui importe c'est de savoir que les logarithmes existent, que nous utilisons majoritairement les log de base 10 et que ces derniers sont facilement accessibles par l'intermédiaire d'une touche spécifique sur la calculatrice. 

Nombre de visites depuis le 19/01/2001 :

Retour vers la page d'accueil du traité
Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP