| Voilà
bien une antenne étrange... D'ailleurs pour être rigoureux, il
conviendrait de spécifier : antenne à réflecteur parabolique. On en
voit fleurir partout (levez les yeux, vous allez constater) et
naturellement on associe ce disque aux très hautes fréquences. Voyons
les comment et pourquoi de son existence. |
|
|
|

|
Présentation :
Voilà l'engin !
Ce modèle n'est pas destiné au grand public ni même aux radioamateurs
mais l'idée est là. On en trouve de toutes les tailles, de tous les types,
on y reviendra. Intuitivement, vous vous doutez bien que cet engin n'est pas
utilisé pour faire des QSO sur 40 mètres et que les spécificités de
cette antenne à réflecteur parabolique sont telles que son domaine de
prédilection va se situer sur des fréquences très hautes. Notez au
passage que vous retrouvez des paraboles un peu partout, comme dans vos
phares d'automobile par exemple.
Un peu de mathématiques :
Pas trop quand même, il est
toutefois intéressant de noter tout de suite quelques propriétés
extrêmement intéressantes et qui font d'ailleurs le succès de ce
réflecteur. Nous allons entrer directement dans le vif du sujet en
court-circuitant quelques notions secondaires pour nous et en abordant la
question sous l'aspect pratique.
|
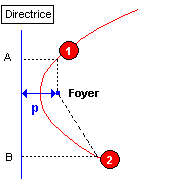 Voici
une jolie parabole représentée verticalement comme pourrait l'être une
antenne... Nous allons noter quelques points importants : Voici
une jolie parabole représentée verticalement comme pourrait l'être une
antenne... Nous allons noter quelques points importants :
*** La droite AB est appelée directrice de
la parabole
***
On trouve un point appelé "Foyer"
et l'on notera que si l'on prend un point quelconque sur la parabole (en
rouge), la distance entre ce point et le foyer est identique à la distance
entre ce point et la directrice.
(j'ai pris deux points quelconques pour illustrer cela, ils sont repérés 1
et 2).
*** La distance "p" est appelée le paramètre de la
parabole.
|
|
|
Equation réduite de la parabole :
|
|
Si vous aimez Excel, vous allez pouvoir
simuler quelques jolies paraboles. Voici l'équation simplifiée :
|
Avec :
x = rayon de la parabole
p = paramètre de la parabole
|

|
|
|
Détermination du foyer :
|
La formule ci-dessus est bien sympathique mais
guère utile en pratique, car en tant que radioamateur, on a plus tendance
à récupérer des paraboles qu'à les concevoir. Une formule simple nous
permet à partir de deux dimensions que nous allons relever sur le disque de
déterminer le point focal:
|
|
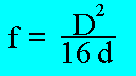
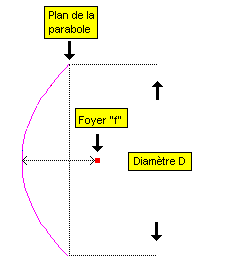
f : distance du foyer par rapport
au fond de la parabole
D : diamètre de la parabole
d : profondeur de la parabole
|
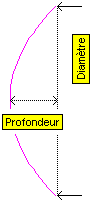
Votre perspicacité ne vous égare pas, il n'a
pas été spécifié d'unité (m, cm, mm) dans la mesure ou si vos unités
sont cohérentes, que vous fassiez le calcul en centimètres, kilomètres ou
UA (unité astronomique) le résultat sera identique. Veillez seulement à
ne pas mélanger les torchons et les serviettes.
|
|
|
|
|
|
|
|

Et la radio dans tout cela ?
Bonne question car ce qui nous intéresse
c'est de savoir comment cela fonctionne, quelles sont les performances etc.
Tout est là... Supposons que nous raisonnions avec de la lumière pour se
raccrocher à quelque chose de quotidien et connu. Le flux lumineux,
représenté par des rayons parallèles traverse le plan de la parabole et
va heurter le fond de celle-ci. A cet endroit, les photons sont réfléchis
vers le foyer (c'est la courbure de la parabole qui réalise ce miracle !).
Ceci est naturellement vrai pour tout rayon entrant, quelle que soit sa
position. On pourrait penser à tort qu'il puisse y avoir des avances ou
retards de phase entre signaux partis au même moment. Notez, voire mesurez
avec une règle que la somme des segments (a1 a2) et (a2 a3) est identique à
la somme des segments (b1 b2) et (b2 b3). Tous les rayons lumineux vont
être "focalisés" vers ce point magique qu'est le foyer. Bien
évidement ce qui est vrai dans le sens réception est également vrai dans
le sens émission dans ce dernier cas, l'énergie sort du point focal (on
verra plus tard comment) puis est réfléchie suivant les mêmes principes.
|
|
|
|
|
|
|
Nous avons le réflecteur mais ce n'est
toujours pas une antenne !
|
|
 ah
oui car pour que cette jolie gamelle puisse se comporter en antenne digne de
ce nom, il faut un élément actif, le réflecteur parabolique n'étant ...
qu'un réflecteur. Ceci nous amène lentement mais sûrement vers la notion
d'illumination. Nous allons donc installer au point focal quelque chose que
nous connaissons bien et qui sera capable de convertir de l'énergie de
rayonnement en tensions électriques et réciproquement. Cette
"source" pourra être un dipôle demi-onde, un cornet, une
hélice, chaque source aura ses spécificités et imprimera à l'ensemble
source-réflecteur des caractéristiques précises. ah
oui car pour que cette jolie gamelle puisse se comporter en antenne digne de
ce nom, il faut un élément actif, le réflecteur parabolique n'étant ...
qu'un réflecteur. Ceci nous amène lentement mais sûrement vers la notion
d'illumination. Nous allons donc installer au point focal quelque chose que
nous connaissons bien et qui sera capable de convertir de l'énergie de
rayonnement en tensions électriques et réciproquement. Cette
"source" pourra être un dipôle demi-onde, un cornet, une
hélice, chaque source aura ses spécificités et imprimera à l'ensemble
source-réflecteur des caractéristiques précises.
Sur cette image, on aperçoit clairement la source montée au foyer de la
parabole ainsi que la mécanique associée, (la source, hélas, ne lévite
pas et c'est bien dommage).
|
|
|
|
|
|
|
Quelques systèmes d'alimentation :
|
|
On peut alimenter par différent
moyens, les plus classiques sont le cornet qui peut être circulaire ou
conique, le patch, l'hélice.
Ce dessin est censé représenter un cornet circulaire (désolé, je ne suis
vraiment pas doué en dessin, de plus je ne vois pas dans l'espace ce qui
m'a et me pose toujours des pb en particulier avec les meubles en kit!
humour...). Grosso modo il s'agit d'une boite qui peut être de diamètre
constant ou pas, de dimensions adéquates et dans laquelle à une distance
du fond judicieuse, on a installé un monopole, lequel est relié à une
fiche coaxiale. Nous venons de réaliser la transition "guide
d'onde-coaxial". On trouve également des cornets pyramidaux
 comme
celui que j'ai tenté de représenter ici. (pas trop mal réussi
d'ailleurs...). Le principe est le même. On trouve également des
alimentations par hélice qui produisent une polarisation circulaire droite
ou gauche en fonction du sens de rotation des spires. Il est également
possible, à partir d'un cornet et moyennant l'utilisation de deux
monopoles, de créer une polarisation circulaire ou une commutation
horizontale/verticale. Si vous êtes intéressé par le sujet, fouinez sur
le web, il y a de la documentation disponible. comme
celui que j'ai tenté de représenter ici. (pas trop mal réussi
d'ailleurs...). Le principe est le même. On trouve également des
alimentations par hélice qui produisent une polarisation circulaire droite
ou gauche en fonction du sens de rotation des spires. Il est également
possible, à partir d'un cornet et moyennant l'utilisation de deux
monopoles, de créer une polarisation circulaire ou une commutation
horizontale/verticale. Si vous êtes intéressé par le sujet, fouinez sur
le web, il y a de la documentation disponible.
|
|
|
|
|
Gain théorique d'une parabole :
|
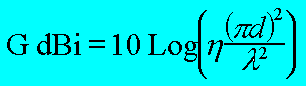 avec
: avec
:
d = diamètre en m
l =
longueur d'onde en m
h =
rendement (comptez 50%)
Log = Log base 10
G en dBi
|
|
D'après cette formule, il apparaît
que le gain de la parabole est lié d'une part à son diamètre,
plus ce dernier est important, plus le gain croît, d'autre part à la
fréquence d'utilisation. Plus la fréquence croît (la longueur d'onde
diminue), plus le gain augmente. Ceci explique que ce type d'antenne trouve
son application dans le domaine 1-30 GHz.

Voici une simulation du gain d'une parabole de 1 m de diamètre.
Intéressant de constater qu'elle ne devient vraiment concurrentielle en
termes de gain vis à vis d'une Yagi qu'à partir des fréquences > à
1,5 GHz. Une parabole de 1 m, je le rappelle, est déjà un bel engin pas si
facilement manoeuvrable que cela, pensez-y si vous habitez dans une région
ventée comme moi. Dans cette simulation, le rendement a été choisi à
50%.
|
|
|
|
|
|
|
La profondeur d'une parabole :
|
|
 Il
s'agit de l'incontournable rapport f/D qui exprime la profondeur d'une
antenne, f représentant la distance focale et D le diamètre de la
parabole. Ce rapport en fonction de sa valeur détermine si nous avons
affaire à une parabole peu profonde (shallow) ou profonde (deep). On retient que
si f/D <0,33 il s'agit d'une antenne profonde et si f/D > 0,36, il
s'agit d'une antenne peu profonde. Ceci va amener à des considérations
importantes en termes d'illumination de la parabole. Une parabole profonde a
son point d'illumination proche du réflecteur ce qui induit une certaine
difficulté à totalement illuminer celui-ci. Bien sûr, l'illumination est
plus facilement atteinte sur une parabole peu profonde mais celle-ci est
plus sujette à recevoir du bruit terrestre aux basses élévations. Il
s'agit de l'incontournable rapport f/D qui exprime la profondeur d'une
antenne, f représentant la distance focale et D le diamètre de la
parabole. Ce rapport en fonction de sa valeur détermine si nous avons
affaire à une parabole peu profonde (shallow) ou profonde (deep). On retient que
si f/D <0,33 il s'agit d'une antenne profonde et si f/D > 0,36, il
s'agit d'une antenne peu profonde. Ceci va amener à des considérations
importantes en termes d'illumination de la parabole. Une parabole profonde a
son point d'illumination proche du réflecteur ce qui induit une certaine
difficulté à totalement illuminer celui-ci. Bien sûr, l'illumination est
plus facilement atteinte sur une parabole peu profonde mais celle-ci est
plus sujette à recevoir du bruit terrestre aux basses élévations.
|
|
|
|
|
La triste réalité :
|
Comme toujours dans la vie, il y a la théorie
et la pratique et l'antenne parabolique n'est pas si facile que cela à
dompter. Nous allons examiner quelques facteurs susceptibles de réduire le
gain théorique.
|
|
|
De la difficulté de bien illuminer une
parabole :
|
|
Supposons que nous
utilisions notre antenne parabolique en émission. Notre énergie haute
fréquence alimente un dipôle demi-onde (sur 10 GHz, ce n'est pas énorme)
ou un cornet peu importe. Ce cornet ou ce dipôle va irradier l'énergie
vers le réflecteur, jusque là tout va bien... Mais ce dont il faut prendre
conscience c'est que l'élément actif n'est pas parfait et qu'il va lui
aussi comme toute antenne avoir des lobes de rayonnement, une ouverture à 3
db etc. Voyons cela en image, ce sera plus simple :
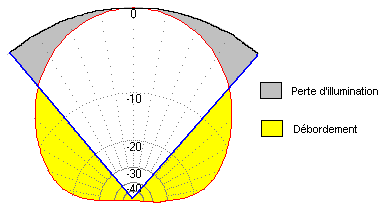 Voici
la chose un peu stylisée et exagérée pour les besoins de la
démonstration. La partie extérieure noire représente le réflecteur, la
pointe du triangle quant à elle représente le foyer où se trouve la
source. On constate que le réflecteur n'est pas totalement illuminé (plus
d'énergie au centre que sur les côtés) , on qualifiera ces pertes de
pertes d'illumination. On note également que le lobe de rayonnement de la
source est bcp trop large et déborde du réflecteur, cette énergie est
perdue. On appellera ce dernier type de perte le Spillover ou en français le
débordement. Voici
la chose un peu stylisée et exagérée pour les besoins de la
démonstration. La partie extérieure noire représente le réflecteur, la
pointe du triangle quant à elle représente le foyer où se trouve la
source. On constate que le réflecteur n'est pas totalement illuminé (plus
d'énergie au centre que sur les côtés) , on qualifiera ces pertes de
pertes d'illumination. On note également que le lobe de rayonnement de la
source est bcp trop large et déborde du réflecteur, cette énergie est
perdue. On appellera ce dernier type de perte le Spillover ou en français le
débordement.
|
|
|
|
|
|
|
Les facteurs réduisant le gain d'une
antenne parabolique :
- Précision de la forme, c'est important.
Aucune parabole ne respecte scrupuleusement la forme idéale, d'autres
se déforment sous les contraintes mécaniques. On imagine facilement
que si la forme n'est plus correcte, la réflexion ne le sera plus
également et n'atteindra plus le foyer.
- Etat de surface de la parabole
- La source et son support obstrue une
partie des signaux arrivant ou partant du réflecteur, on a trouvé la
parade en construisant la parabole offset. Cet inconvénient et d'autant
plus marqué que le réflecteur est petit.
- Les pertes diverses et variées entre le
système d'alimentation et la source.
- La dissymétrie entre les champs
magnétique et électrique.
- Diffraction sur les bords du
réflecteur.
- Illumination incorrecte.
Bref, ce n'est aussi simple qu'il y paraît.
|
|
|
|
|
|
|
La parabole Offset:
|
|

Jusqu'ici nous n'avons travaillé que sur la
parabole dite "Prime Focus" ou à foyer primaire. Nous venons de
voir qu'un des grands inconvénients de ce type de réflecteur est que
la source et sa fixation se trouvent au foyer dans l'axe de la parabole, ce
qui contribue à masquer les signaux et à diminuer le gain. Un réponse
intelligente est apportée par la parabole "Offset" rendue
célèbre par sa diffusion à des prix ridicules pour la réception TV par
satellite. Le réflecteur est constitué par une portion de parabole ce qui
a pour immense avantage de dégager le foyer de l'axe. Ceci est clairement
visible sur l'image ci-contre. Notez également la position de la parabole
pour recevoir des signaux sur l'horizon. Sans entrer dans des
considérations complexes qui n'ont pas leur place ici, les méthodes de
calcul pour déterminer le foyer et le diamètre de ce type de parabole sont
naturellement différents de ceux décrits pour la prime focus. Vous
trouverez une abondante documentation concernant ce dernier point sur le
web.
|
|
|
|
|
Pour les pros : la parabole type
Cassegrain :
|
|
 Ce
type de réflecteur est quand même plus complexe que ce que nous avons vu
jusqu'à présent, pas tant par le principe que par la réalisation
mécanique. On réserve généralement ce type de montage pour des paraboles
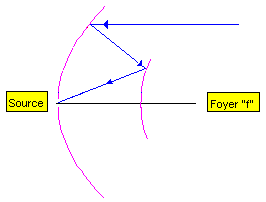
assez grandes. Voici le principe : Ce
type de réflecteur est quand même plus complexe que ce que nous avons vu
jusqu'à présent, pas tant par le principe que par la réalisation
mécanique. On réserve généralement ce type de montage pour des paraboles
assez grandes. Voici le principe :
L'énergie arrive sur le plus grand réflecteur, y est normalement
réfléchie vers le foyer "f" qui est commun aux deux
réflecteurs. Le second réflecteur (notez que dans ce cas de figure il est
convexe alors que le réflecteur primaire est concave) réfléchit cette
énergie vers le foyer dans lequel est installée la source. Ce type de
montage offre des avantages en termes d'illumination, de débordement, de
gain global et ce malgré le léger effet de masque du second réflecteur.
Ceci se paie par une complexité mécanique accrue et des tolérances de
réalisation serrées. Le schéma ci-contre n'est pas à l'échelle, le
réflecteur secondaire est bcp plus petit que ce que ne laisse apparaître
le dessin.
|
|
|
|
| Nous
n'avons pas fait le tour de la question, loin s'en faut, toutefois une
savons maintenant quelles sont les performances que l'on peut en attendre
et les difficultés de mise en oeuvre dans le cadre de nos activités
amateur. |
![]()
 Voici
une jolie parabole représentée verticalement comme pourrait l'être une
antenne... Nous allons noter quelques points importants :
Voici
une jolie parabole représentée verticalement comme pourrait l'être une
antenne... Nous allons noter quelques points importants :
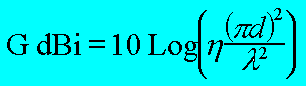 avec
:
avec
: