Circuits "parallèle"

Nous avons vu comment calculer l'impédance d'un circuit série dans le précédent chapitre. Si les circuits série sont assez simples à étudier, il n'en est pas de même avec les circuits parallèle. Notre étude sera donc limitée car au prochain chapitre, je vous présenterai une méthode simple bien qu'un peu fastidieuse applicable à tous les circuits pour déterminer impédance et déphasage.
Le circuit :
Voilà l'engin, il est plus théorique que pratique car la self  qui est toujours résistive devrait être représentée avec une résistance série. On voit vite que dans ce circuit, l'élément commun sera la tension et que les courants circulant dans chaque branche n'auront pas la même phase.
Pourquoi les circuits // sont-ils plus compliqués à analyser que les circuits série ?
Vous vous souvenez du calcul des résistances en //, vous étiez obligé de passer par l'inverse de la résistance  pour pouvoir calculer la résultante , puis de nouveau passer par l'inverse pour obtenir la résistance équivalente. Il en est de même ici mais avec des réactances.		Retenez que l'inverse de la résistance s'appelle la conductance               1 G =  _______                R
Passons à notre circuit:
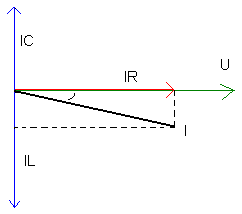
Nous allons utiliser l'axe des tension comme référence et tracer les différents vecteurs représentatifs du courant circulant dans chaque branche. IL sera le courant dans la self IR sera le courant dans la résistance IC sera le courant dans le condensateur I sera le courant résultant U la tension aux bornes
Comme vous pouvez le constater, rien de nouveau sous le ciel de l'électricité. On notera toutefois que :		IR est en phase avec U IL est en retard de 90° sur U IC est en avance de 90° sur U
Si nous voulons connaître la valeur du courant total, nous passerons inéluctablement par une addition vectorielle		__     __   __    __ IT =  IR + IL + IC La barre supérieure indique un vecteur
Voyons ce qui se passe sans les vecteurs:
Nos souvenirs de la loi d'Ohm nous disent que I = U/R d'une part et d'autre part que le courant dans la self IL = U/X soit IL =  U/ Lw . Le courant dans le condensateur IC sera égal à   IC = U/X soit IC=  U/ (1/Cw) soit : IC = U/Cw		Le courant dans la résistance sera quant à lui I = U/R. Si nous posons : I2 =  IR2 + ( IL - IC)2 Nous sommes toujours dans le vrai.
Et si nous bricolons en remplaçant  I par sa valeur tirée de la table ci-dessus on obtient :		I2 =  U2 /R2 +  ( U/Lw   -  UCw)2 mettons U en facteur I2  =  U2 [1/R2 + ( 1/Lw-Cw)2 ]     Il ne reste plus qu'à tirer la racine et nous obtenons I et du coup la valeur de l'impédance du circuit Z.
Impédance du circuit parallèle à la résonance :
	Z = R	Nous allons grandement simplifier les choses en abordant uniquement et assez schématiquement l'impédance du circuit // à la résonance. C'est un chapitre ultérieur mais je présume que vous avez déjà une petite idée sur la question. Donc, à la résonance, les courants dans L et C sont identiques mais opposés, il ne reste plus en terme d'impédance que la valeur de la résistance.
Voyons un cas particulier pourtant très réel :
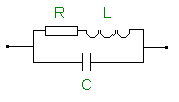Voici la situation : Nous nous retrouvons en présence d'une self ayant une résistance ohmique ce qui est la réalité physique car aussi petite soit-elle, cette résistance existe. L'ensemble se trouve en parallèle avec un condensateur. Nous nous proposons de déterminer l'impédance à la résonance. Pour réaliser ce prodige, on passe par une transformation du circuit série en parallèle et on aboutit à :
ou		Z : ohm L : inductance en H W : 2 p f R : ohm Q : coeff de qualité Xl : réactance de L en ohm
Fin de ce chapitre présentant les circuits //, nous en verrons les caractéristiques importantes dans les chapitres suivants

 Nombre de visites depuis le 19/01/2001 :

Retour vers la page d'accueil du traité

Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP

Révision 01 du 17/10/2001